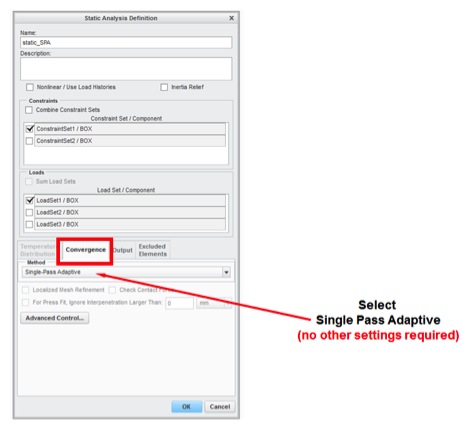
The Single-Pass Adaptive (SPA) convergence criteria are setup using the Analysis Definition data form. Setting up SPA convergence is very simple; just select the SPA option on the convergence tab and you are done. This convergence method is easy to setup and generally runs much faster than the MPA convergence method. This method should be used for most of the design iteration process when a good solution is sufficient but a verifiable or know accuracy is not required.
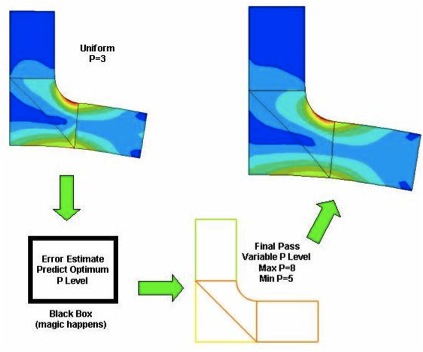
This algorithm is not a convergence process at all. This algorithm performs only single error checking pass between two solution passes. For the first pass all the elements edges are set to a uniform polynomial level (P-level) 3 or third order. After the first solution pass the algorithm performs error estimation throughout the model. It estimates the maximum P-level required everywhere in the model to obtain a good solution. The element P-levels are set to these values and the final or second solution pass is made.
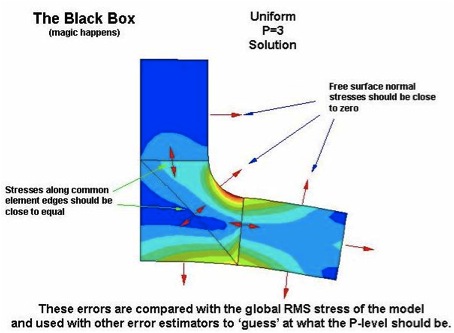
The user has no control over the accuracy of the solution, so, how does it work and why should you use it (or not)? If you return to the FEA Basics section and note that each element calculates its own stress field based on the deformed shape of each element, you will have a good basis for understanding how the error estimation is made. Since each element calculates the stress field independently from the others, the stress field across the entire mesh is not continuous. Stresses along common edges between elements will each calculate a different stress. If the solution is good, the stresses should be close. If the solution is not so good, the stresses will be much different. This is used as a basis for estimating solution error locally in the model. Also, stress components normal to the free unconstrained surfaces should be zero. Due to solution error they never are. How close they are to zero is another basis for the error estimation. These errors and other criteria are compared with the overall RMS stress in the model and, along with empirically derived fudge factors, are used to determine the P-level for the final pass. The algorithm was optimized with the goal of obtaining as good or better result with this algorithm as would be obtained using the Multi-Pass Adaptive (MPA) convergence algorithm setup with the default criteria.
The advantage to this algorithm is that it has been shown to be as much as 30 times faster than the MPA algorithm. The disadvantage is that you have no control over accuracy and very little feedback on the level of accuracy achieved.
For modal analysis SPA convergence is based on the stresses calculated for the normalized deformed mode shapes. For a thermal analysis the SPA uses Heat Flux rather than stress for error estimation.
Accuracy Issues with Single-Pass Adaptive Convergence
Most of the time you will get better and faster solutions with the SPA convergence than with MPA. This is especially true if you are interested in the maximum stress in the model. That is because the error estimation process is stress based.
Models run using SPA convergence are sensitive to the same issues as MPA solutions. These include:
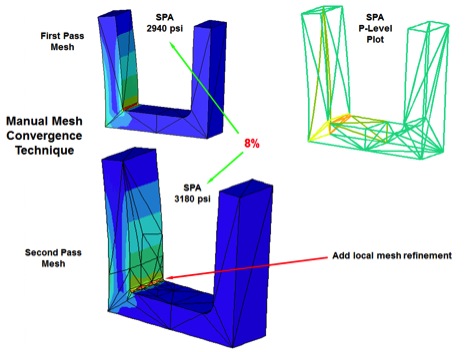
If you suspect a high stress gradient problem or a poorly shaped element problem you will need to use the method of mesh refinement talked about and re-run the solution to check for any change in the result. Usually one or two iterations are all that will be required.
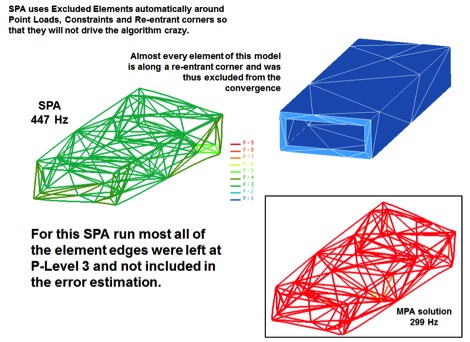
There is a unique problem using SPA with models that have re-entrant corners, point loads, edge loads or any constraints. That problem is that the SPA algorithm recognizes these as possible singularities and excludes any elements from the error estimation that touch these singularities. In some models this can be extremely significant. Most affected will be the overall stiffness of the structure. You can detect the problem first by looking at the summary report. If the number of equations between pass 1 and pass 2 does not increase by much (approx. < 20%) then there may be a significant number of elements being ignored during the error estimation. Another clue is to look at the P-level plots. If most of the model is at P-level 3 then there may also be a significant number of elements being excluded. The solution to this problem is to use MPA, add fillets or use the ‘Isolate for Exclusion’ option under Mesh Control.
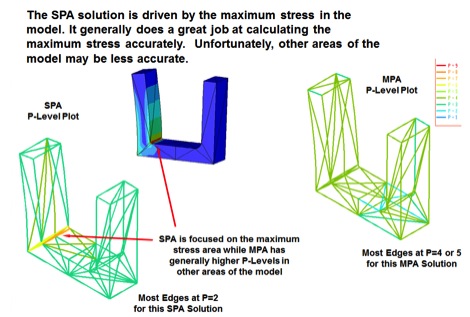
The SPA algorithm is driven by the maximum stress in the model. Generally it does a great job calculating these maximum stresses, however, if there are only very few areas of high stress with large stress gradients, other areas of the model may not provide as accurate of results. It has been found that stresses and deflections in lower stress areas of the model may be as much as 30% off. You may recognize these potential problems if your stress plots have only one or two very localized high stress gradient areas and everything else is at a much lower stress level. The solution to this problem is to run it using MPA.