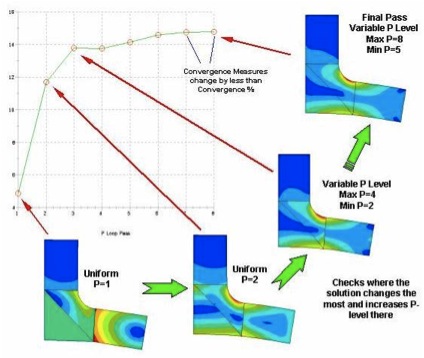
The Multi-Pass Adaptive (MPA) convergence algorithm uses multiple solution steps, increasing the total degrees-of-freedom (DOF) with each step until user specified measures have converged. This convergence method provides the user with the greatest control and is best used if the accuracy of the solution is critical.
The algorithm starts the first pass with a uniform polynomial level (P-Level) for all element edges. The default is first order or linear equations. The P-level is increased uniformly to the next order for the second pass. This raises the total DOF for the model. The algorithm then checks locally in the model where the strain energy and displacements have changed the most. In those areas it will increase the P-level again and run another solution pass. This locally adaptive P-level is something that is unique to Creo Simulate P-element technology. After this third pass the algorithm will again check locally for where the greatest change occurred and where the P-level may be increased again. It will also start checking convergence of user specified measures and convergence tolerance. If the user specified measures have changed by less than the percent convergence tolerance between the last and previous pass, the algorithm will declare the solution converged and end the process. If the measures have not converged, the algorithm will continue with the process.
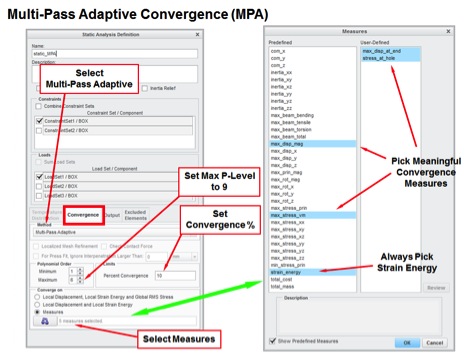
The MPA convergence criteria are setup using the Analysis Definition data form. After selecting MPA convergence from the convergence tab, set the maximum P-level to 9th order. The default is 6th. The default is 6th because the mathematics gurus at PTC feel that the best meshed models will converge before P-level 6. This may be true but from a practical point of view you will have time saved if you let it go to 9th rather than re-mesh and try again.
Next you select the measures you are interested in converging on. You should pick measures that are meaningful to the problem and leave others alone. For example if you were interested in the deflection of an end-loaded cantilever beam you would pick the displacement in the direction of load. You would not pick the other displacements in other directions if the beam does not want to bend that way. This is because their values will be very small and may change in magnitude by more than the percent convergence selected. A displacement of 1e-9 may be as close to zero as 1e-12 in your mind but to the MPA algorithm they are 1000 times different. You should always pick Strain Energy as convergence criteria. Theoretically you do not have a good solution unless the strain energy has converged. After selecting the measures, set the percent convergence you would like to achieve. The lower the percent the longer it may take to run. The default is 10%, which should give you a good ballpark number.
Fixing Convergence Problems
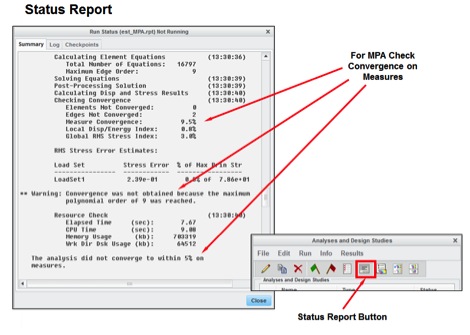
Sometimes your solutions may not converge. The first and most obvious indication of this would be shown in the Run Status window under the Summary tab. There will be a statement in this window indicating if your convergence criteria has been met.
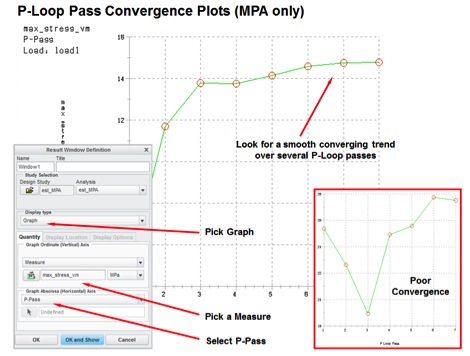
Often times the solution will appear to converge based on your setup criteria, but, the solution may not have ‘good’ convergence. The next step is to look at the convergence plots for the results of interest. If you are interested in stress, then look at the stress convergence plots. If you are interested in displacements, then look at displacements convergence plots.
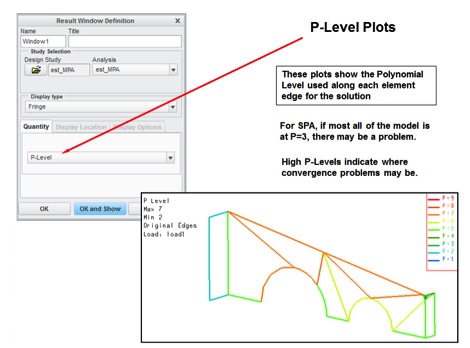
Once you have determined that there is a convergence problem you will need to identify the area in the model where the problem exists. P-level plots may help narrow this down. The areas in the model that have the highest P-level will probably be where you want to focus.
Common convergence problems and methods to deal with them are shown in the links below.